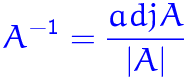
One day, my officemate Tieming asked me about a problem that she met in her research. Suppose \(\boldsymbol{B}\) is a symmetric matrix of huge dimension and \(\boldsymbol{D}\) is a diagonal matrix with nonnegative diagonal elements. The inverse of \(\boldsymbol{B}\) is already known, how can we calculate the …

Suppose we flip a coin which has probability 0.7 to be head again and again and two people choose two different sequences of length 3 (e.g., THH). The people whose sequence appears first wins. If you are allowed to choose first, which sequence will you choose?

I discussed …

Suppose you toss a symmetric dice. You are allowed to quit the game and get money which equals the total points you get at any time if 6 has never showed up. Whenever 6 shows up, the game is over and you get nothing. For example, if the first three …

I found this "probability" problem when I read a person's blog.

What's probability that two randomly chosen nature numbers are relatively prime?

It is claimed that there is a very elegant solution for this problem. This problem reminds me another one. Some people asked for an example of a 0-probability …

If we randomly put balls into \(m(\ge1)\) boxes until \(n(\le m)\) of them are occupied, what is the expectation of the number of balls needed?

See my neat solution here.

Suppose there are \(n\) distinct numbers \(x_1,\ldots, x_n\), and \(y_1, \ldots, y_n\) is a random permutations of them. If \(\exists k\) such that \(y_k<y_i, \forall 1\le i<k\), then we say that \(y_k\) is a record (we always count \(y_1\) as a record). What is the expected …