Stick Breaking Problems

The following is a popular brain teaser problem about probability.

Randomly select two points on a unit stick to break it into 3 pieces, what is the probability that the 3 pieces can form a triangle?

The critical thing here is how are the two points selected. The most popular (and probably default) way is that $X_1, X_2 \overset{iid}{\sim} U(0, 1)$, where $X_1$ and $X_2$ are the distances from the two points to the left end of the stick. There some other interesting ways of selecting the points, and I will study the 3 cases in this post.

Independent Uniformly Distributed

Let $X_1$ and $X_2$ be the distances from the two points to the left end of the stick. In this situation we assume that $X_1, X_2 \overset{iid}{\sim} U(0, 1).$

Method I: Exclusive Method

Let $l_1$, $l_2$ and $l_3$ be the lengths of the 3 pieces from the left end of the stick. To form a triangle, $l_1$, $l_2$ and $l_3$ have to satisfy the following conditions.

$$l_1 + l_2 > l_3,$$

$$l_2 + l_3 > l_1,$$

$$l_3 + l_1 > l_2.$$

Or equivalently,

$$0 < l_1, l_2, l_3 < \frac{1}{2}.$$

\begin{align} P_{\bigtriangleup} &= P(0 < l_1, l_2, l_3 < \frac{1}{2}) \nonumber \newline &= 1 - P(l_1 \ge \frac{1}{2} | l_2 \ge \frac{1}{2} | l_3 \ge \frac{1}{2}) \nonumber \newline &= 1 - \left(P(l_1 \ge \frac{1}{2}) + P(l_2 \ge \frac{1}{2}) + P(l_3 \ge \frac{1}{2})\right). \nonumber \newline \end{align}

\begin{align} P(l_1 \ge \frac{1}{2}) &= P(min\\{X_1, X_2\\} \ge \frac{1}{2}) = P(X_1 \ge \frac{1}{2}, X_2 \ge \frac{1}{2}) \nonumber \newline &= P(X_1 \ge \frac{1}{2}) P(X_2 \ge \frac{1}{2}) \nonumber \newline &= \frac{1}{2} \times \frac{1}{2} = \frac{1}{4}. \nonumber \end{align}

$l_3$ is symmetric to $l_1$, so $P(l_3 \ge \frac{1}{2}) = \frac{1}{4}$.

It can be shown (see Method II) that $P(l_2 \ge \frac{1}{2}) = \frac{1}{4}$, so

\begin{align} P_{\bigtriangleup} &= 1 - \left(P(l_1 \ge \frac{1}{2}) + P(l_2 \ge \frac{1}{2}) + P(l_3 \ge \frac{1}{2})\right) \nonumber \newline &= 1 - \left(\frac{1}{4} + \frac{1}{4} + \frac{1}{4}\right) = \frac{1}{4} = 0.25. \nonumber \end{align}

Method II: Visualization

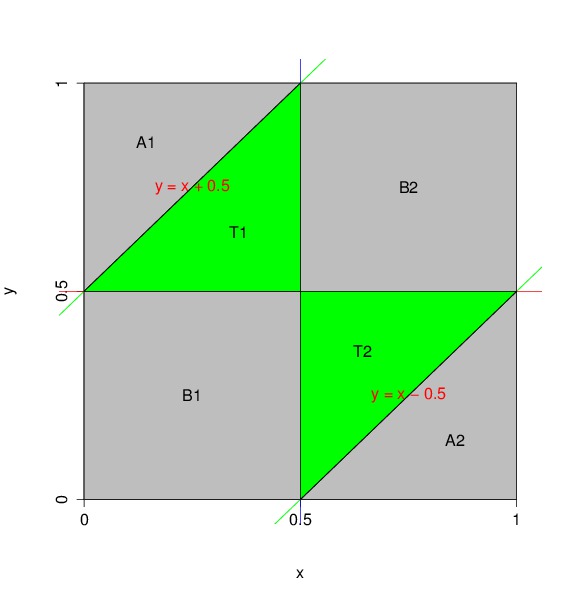
Figure 1: Probability to Form a Triangle.

Let $X_1$ and $X_2$ be defined as above. For the convenience of visualization, Figure 1 uses $X$ to stand for $X_1$ and $Y$ to stand for $X_2$. The pair $(X, Y)$ is uniformly distributed in the unit square $[0,1] \times [0,1]$ as shown in Figure 1. To form a triangle, $X$ and $Y$ need to satisfy the following conditions.

\begin{align} |X - Y| &< \frac{1}{2}, \newline (X - \frac{1}{2}) & (Y - \frac{1}{2}) < 0 \end{align}

Condition (1) requires that the middle part of the 3 pieces cannot be greater than $\frac{1}{2}$. It is equivalent to

\begin{align} Y &> x - \frac{1}{2}, \newline Y &< x + \frac{1}{2}, \end{align}

which corresponds to the hexagon in the middle of the unit square (consisting of $B_1$, $B_2$, $T_1$ and $T_2$). Condition (2) requires that $X$ and $Y$ cannot be both smaller than $\frac{1}{2}$ or bother greater than $\frac{1}{2}$, which excludes areas $B_1$ and $B_2$. So when $X$ and $Y$ falls into $T_1$ or $T_2$ (grean areas), the 3 pieces of sticks can form a triangle. It is easy to see that the area/probability is $\frac{1}{4}$.

Let $l_1$, $l_2$ and $l_3$ be defined as in Method I. $l_1 > \frac{1}{2}$ corresponds to the area $B_2$ whose area/probability is $\frac{1}{4}$; $l_2 > \frac{1}{2}$ corresponds to the areas $A_1$ and $A_2$. Their areas/probabilities sums to $\frac{1}{4}$. $l_3 > \frac{1}{2}$ corresponds to the area $B_1$ whose area/probability is $\frac{1}{2}$.

The R code used to generate Figure 1 is given below.

par(col="black", lty="solid")
# an empty plot without axes
plot(c(0,1), c(0,1), type="n", axes=F, xlab="x", ylab="y")
# add a square 
rect(0, 0, 1, 1)
# add x and y axes
at = c(0, 1/2, 1)
lab = c("0", "0.5", "1")
axis(1, pos=0, at=at, labels=lab)
axis(2, pos=0, at=at, labels=lab)
# add 2 green lines with slope 1
abline(1/2, 1, col="green")
abline(-1/2, 1, col="green")
# add a vertical line
abline(v=1/2, col="blue")
# add a horizontal line
abline(h=1/2, col="red")
# top left triangle, grayed
x = c(0, 0, 1/2)
y = c(1, 1/2, 1)
polygon(x, y, col="gray")
# bottom right triangle, grayed
x = c(0.5, 1, 1)
y = c(0, 0, 0.5)
polygon(x, y, col="gray")
# bottom left and top right squares, grayed
x = c(0, 1/2, 1/2, 1, 1, 0)
y = c(0, 0, 1, 1, 1/2, 1/2)
polygon(x, y, col="gray")
# add 2 inner green triangles
x = c(0, 1, 1/2, 1/2)
y = c(1/2, 1/2, 0, 1)
polygon(x, y, col="green")
# flag the top left gray triangle as A1
text(1/7, 6/7, labels="A1")
# flag the bottom right gray triangle as A2
text(6/7, 1/7, labels="A2")
# flag the bottom left gray square as B1
text(1/4, 1/4, labels="B1")
# flag the top right gray square as B2
text(3/4, 3/4, labels="B2")
# flag the 2 inner green triangles as T1 and T2
text(1/2-1/7, 1/2+1/7, labels="T1")
text(1/2+1/7, 1/2-1/7, labels="T2")
# label the (upper) green line y = x + 0.5
text(1/4, 3/4, labels="y = x + 0.5", col="red")
# label the (lower) green line y = x - 0.5
text(3/4, 1/4, labels="y = x - 0.5", col="red")

Method III: Order Statistics

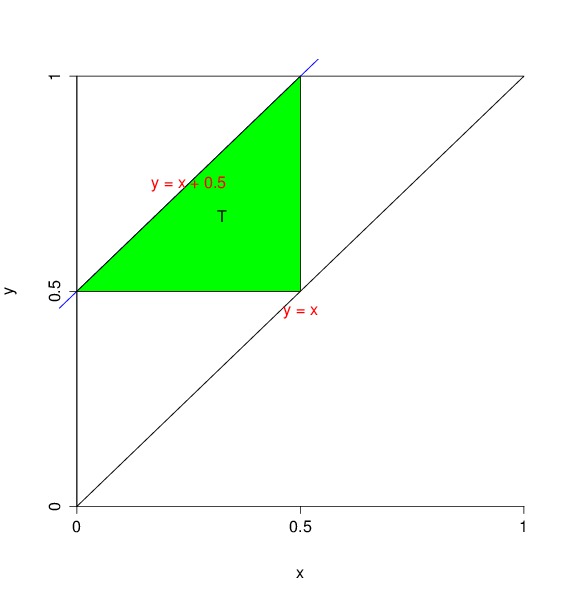
Let $X_1$ and $X_2$ be as defined above. Let $X_{(1)} = min\{X_1, X_2\}$ and $X_{(2)} = max\{X_1, X_2\}$, then $X_{(1)}$ and $X_{(2)}$ are order statistics. From the theorem of order statistics we know that the join density of $X_{(1)}$ and $X_{(2)}$ is constant 2 with support $0 < X_{(1)} < X_{(2)} < 1$. To form an triangle, $X_{(1)}$ and $X_{(2)}$ have to satisfy the following condition.

$$ 0 < x_{(1)} < \frac{1}{2} < X_{(2)} < X_{(1)} + \frac{1}{2}. $$

The probability for the 3 pieces of sticks to form an triangle is thus

\begin{equation} \int_{0}^{\frac{1}{2}} \int_{\frac{1}{2}}^{x_1+\frac{1}{2}} 2\, dx_2\,dx_1 = \int_{0}^{\frac{1}{2}} 2x_1 dx_1 = x_1^2|_{0}^{\frac{1}{2}} = \frac{1}{4}. \end{equation}

The support of the joint density of $X_{(1)}$ and $X_{(2)}$ is the big triangle in Figure 2. For the convenience of visualization, Figure 2 uses $X$ to stand for $X_{(1)}$ and $Y$ to stand for $X_{(2)}$. The integral domain of (5) is the green area T in Figure 2.

The R code to generate Figure 2 is given below.

par(col="black", lty="solid")
plot(c(0,1), c(0,1), type="n", axes=F, xlab="x", ylab="y")
x = c(0, 0, 1)
y = c(1, 0, 1)
polygon(x, y)
segments(1/2, 1, 1/2, 1/2, col="red")
segments(0, 1/2, 1/2, 1/2, col="red")
abline(1/2, 1, col="blue")
at = c(0, 1/2, 1)
lab = c("0", "0.5", "1")
axis(1, pos=0, at=at, labels=lab)
axis(2, pos=0, at=at, labels=lab)
# middle triangle
x = c(0, 1/2, 1/2)
y = c(1/2, 1/2, 1)
polygon(x, y, col="green")
text(1.3/4, 2.7/4, labels="T")
text(1/4, 3/4, labels="y = x + 0.5", col="red")
text(1/2, 0.45, labels="y = x", col="red")

Dependent Uniformly Distributed

Let $X_1$ and $X_2$ be defined as above. In this situation we assume that

$$X_1 \sim U(0, 1),$$

$$X_2 | X_1 \sim U(X_1, 1).$$

\begin{align} P_{\bigtriangleup} &= \int_{0}^{\frac{1}{2}} \frac{1}{1-x_1} \int_{\frac{1}{2}}^{x_1+\frac{1}{2}} dx_2\, dx_1 \nonumber \newline &= \int_{0}^{\frac{1}{2}} \frac{x_1}{1-x_1}dx_1 = log2 - \frac{1}{2} \approx 0.1931. \nonumber \end{align}

The Dirichlet distribution is a distribution that is frequently used in Bayesian non-parametric models. It has a stick-breaking construction. Let $Y_1 = X_1$, $Y_2 = X_2 - X_1$ and $Y_3 = 1 - X_1 - X_2$. The specification of the joint distribution of $Y_1$ and $Y_2$ sounds a lot like a the construction of a Dirichlet distribution, however, it is not! Given $Y_1 = X_1 \sim U(0, 1) \overset{d}{=} B(1, 1)$, if $Y_2 \sim (1-Y_1)B(\alpha, \beta)$, where $\alpha + \beta = 1$, then the joint distribution of $Y_1$, $Y_2$ and $Y_3$ is Dirichlet distribution with concentration parameters 1, $\alpha$ and $\beta$.

Dirichlet Distributed

Let $Y_1$, $Y_2$ and $Y_3$ be defined as above. In this situation we assume that

$$(Y_1, Y_2, Y_3) \sim Dir(1, \frac{1}{2}, \frac{1}{2}),$$

that is

$$X_1 \sim U(0, 1),$$

$$X_2 | X_1 \sim X_1 + (1-X_1) U(\frac{1}{2}, \frac{1}{2}).$$

\begin{align} P_{\bigtriangleup} &= \int_{0}^{\frac{1}{2}} \int_{\frac{1}{2}-x_1}^{\frac{1}{2}} \frac{1}{\pi} x_2^{1/2}(1-x_1-x_2)^{1/2} dx_2\, dx_1 \nonumber \newline &= \frac{2}{\pi} - \frac{1}{2} \approx 0.1366. \nonumber \end{align}

Ben Chuanlong Du's Blog

And let it direct your passion with reason.