Suppose a poker games requires 4 decks of poker. After the game, the cards are put back into the 4 decks randomly. Now there is another game which requires only 1 deck of poker, so we want to open some decks of the poker and find a complete set of cards. Since people are lazy, we do not want to open all the 4 decks of poker. If we open 2 decks of cards, what is the probability that we can get a complete set of cards?
It is hard to solve this specific problem directly. The viewpoint of treating a deck of cards as a whole is especially a barrier for solving this problem. Here is the fancy idea. We can generalize this problem as follows. Suppose there are \(N\) distinct cards in a deck of poker. Now \(M\) decks of pokers are mixed together and then put back. If we draw \(n\) cards randomly, what is the probability that we get \(m\) types (cards of the same color and suit are consider to be the same type) of cards? Now to answer the question that how much chance we can get a complete set of cards if we open \(k\) decks of poker, we just need to calculate the probability of getting \(N\) types of cards, if we draw \(kN\) cards randomly from these mixed cards.
Let's use \(A_{n,m}\) to stand for the event of getting \(m\) types of cards when \(n\) cards are randomly drawn, and \(P_{n,m}\equiv P(A_{n,m})\). Then conditioning on the number of types of cards we get in the first \(n-1\) draws, we have the following recursion formula
We can find a formula for general terms using method of generating functions. Since there are two subscript changing at the same time, it is much harder to solve this recursion formula. However, as I mentioned before, we have actually solved the problem from practical view because we have recursion formula and we know the initial values. We can write a program to help us solve this problem. The following is an implementation of the recursion formula in Mathematica.
GeneralizedHyperGeometryProbability::illegal = "The number of selected exeeds the total number.";
(*
@param nselected: the number of card selected;
@param ndistinct: the number of distinct card in the selected card;
@param Ndistinct: the total number of distinct card;
@param Ncopies: the copies of poker.
*)
GeneralizedHyperGeometryProbability[nselected_, ndistinct_, Ndistinct_, Ncopies_] := Module[
{TotalCardsNumber, TotalChoices, i, j, result = {}, n, nleft},
TotalCardsNumber = Ndistinct*Ncopies;
If[TotalCardsNumber < nselected,
Message[GeneralizedHyperGeometryProbability::illegal];
Return[False]
];
If[Ndistinct < ndistinct, Return[0]];
If[nselected < ndistinct, Return[0]];
If[ndistinct * Ncopies < nselected, Return[0]];
If[ndistinct == 1,
Return[Ndistinct * Binomial[Ncopies, nselected] / Binomial[TotalCardsNumber, nselected]]
];
TotalChoices = Binomial[TotalCardsNumber, nselected];
If[nselected == ndistinct,
Return[Binomial[Ndistinct, ndistinct]*Ncopies^ndistinct/TotalChoices]
];
For[i = 1, i <= ndistinct, i++,
AppendTo[result,
GeneralizedHyperGeometryProbability[i, i, Ndistinct, Ncopies]]
];
For[i = 2, i <= nselected - ndistinct + 1, i++,
result[[1]] = GeneralizedHyperGeometryProbability[i, 1, Ndistinct, Ncopies];
For[j = 2, j <= ndistinct, j++,
n = j - 1 + i;
nleft = TotalCardsNumber - n + 1;
result[[j]] = result[[j]]*(j*Ncopies - n + 1)/nleft + result[[j - 1]]*(Ndistinct - j + 1)*Ncopies/nleft
]
];
Return[result[[ndistinct]]]
]
In[5]:= N[GeneralizedHyperGeometryProbability[54*1, 54, 54, 4]]
Out[5]= 9.19323*10^-20
In[6]:= N[GeneralizedHyperGeometryProbability[54*2, 54, 54, 4]]
Out[6]= 0.0190881
In[7]:= N[GeneralizedHyperGeometryProbability[54*3, 54, 54, 4]]
Out[7]= 0.820296
And the following is another implementation of the recursion formula in R.
#'
#' @param nselected the number of card selected;
#' @param ndistinct the number of distinct card in the selected card;
#' @param Ndistinct the total number of distinct card;
#' @param Ncopies the copies of poker.
#'
pghyper = function(nselected, ndistinct, Ndistinct, Ncopies){
TotalCardsNumber = Ndistinct*Ncopies
if(TotalCardsNumber < nselected)
stop("the number of selected exceeds the total number.")
if(Ndistinct < ndistinct)
return(0)
if(nselected < ndistinct)
return(0)
if(ndistinct * Ncopies < nselected)
return(0)
TotalChoices = choose(TotalCardsNumber, nselected)
if(ndistinct == 1)
return(Ndistinct * choose(Ncopies, nselected) / TotalChoices)
if(nselected == ndistinct){
dchoices = choose(Ndistinct, ndistinct)
multiple = Ncopies ^ ndistinct
if(dchoices < multiple)
return(multiple / (TotalChoices / dchoices))
else
return(dchoices / (TotalChoices / multiple))
}
result = NULL
for(i in 1:ndistinct)
result = c(result, pghyper(i, i, Ndistinct, Ncopies))
for(i in 2:(nselected-ndistinct+1)){
result[1]=pghyper(i,1,Ndistinct,Ncopies)
for(j in 2:ndistinct){
n=j-1+i
nleft=TotalCardsNumber-n+1
result[j]=result[j]*(j*Ncopies-n+1)/nleft
+result[j-1]*(Ndistinct-j+1)*Ncopies/nleft
}
}
result[ndistinct]
}
> pghyper(54*1,54,54,4)
[1] 9.19323e-20
> pghyper(54*2,54,54,4)
[1] 0.01908814
> pghyper(54*3,54,54,4)
[1] 0.8202961
From the above result,
we can see that in the original problem the probability
is only about \(2\%\) for us to get a complete set of cards
if we only open 2 decks of pokers
while the probability is about \(82\%\) if we open one more deck of poker (i.e. open 3 decks of pokers).
So for a really lazy person, it seems that to open 3 decks of poker is a good choice.
Let \(f(k)=P_{54k,54}, k=1,\ldots, 4\).
The above result also suggests us that function \(f(k)\) is a very odd function.
It is small when \(k\) is smaller and then suddenly increases to a (relative) very big value,
and then it increases mildly to 1.
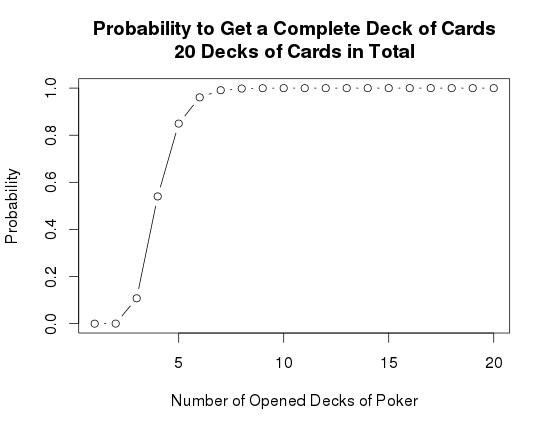
Now suppose there are 20 decks of poker (each has 54 cards) involved,
let's see how function \(f(k)=P_{54k,54}\), \(k=1,\ldots, 20\), behaves.
The plot of the function \(f(k)=P_{54k,54}\), \(k=1,\ldots, 20\),
is shown is in the following figure.
We can see that for very small \(k\), \(f(k)\) is very small;
then \(f(k)\) increase dramatically to a (relative) very big value and then it increase mildly to 1.
For other number of decks of poker, \(f(k)\) has similar properties.
So in this kind of problems, definitely we will not have a big probability to success if open 1 or 2
decks of poker. However, we do not have to open too many decks of poker, e.g., 4 or 5 decks would
yield a remarkable success probability even if many (e.g., 100) decks of pokers are involved.