Suppose a basketball player make \(N\) shots, and we know that in the first \(n(\le N)\) shots he sinked \(m(\le n)\) shots. If from the \((n+1)^{th}\) shot, his ratio of sink a shot is his accumulative ratio before the shot, e.g., suppose he sinked 40 shots in the first 50 shots, then his ratio of sink the next shot is 80%. What's the probability that he will make \(M\) shots finally?

Using the knowledge of permutation and combination, we can solve this problem directly. Let \(E_{m,n}\) be the event that \(m\) success in the first \(n\) shots. It turns out to be that

Notice that

i.e., the number of sinked shots \(M\) is uniformly distributed on its support given that the player only sinked 1 shot in the first 2 shots.

Let \(X_k, n\le k\le N\) be the number of shots the player sinks in the first \(k\) shots, then the distribution of \(X_{k+1}\) conditioning on \(X_{k}\) is given in Table 1. Using the similar method as we've done in the first 3 problems, we can easily find the first and second moment of \(X_k\) which are given below:

So the variance of \(X_k\) is

From the above formulas, we can know that the expectation and variance of the number of sinked shots are linear quadratic functions of \(k\) respectively, and both of them increase as \(k\) increases. This makes it hard for us to predict \(X_k\) when \(k\) is big. The 2-\(\sigma\) intervals for \(X_k\) is shown in the follow figure.

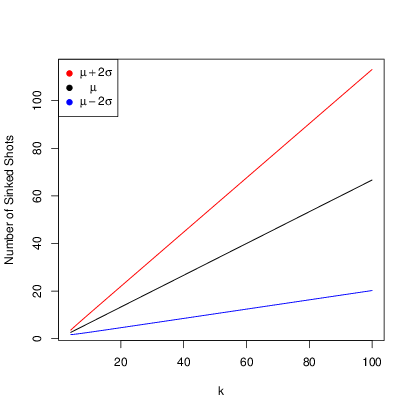
Since we know the distribution of the number of sinked shots given that the player sinked \(m\) shots in the first \(n\) shots, we can calculate the first and second moments directly, which yields the following equations: